Eco-evolutionary dynamics of living systems: Theory
Two studies focused on the individual-based foundations of foraging and growth:
- Unlike plants, animals actively move according to their physiological state and environmental input. EEP researchers examined how reactions to local variations in prey and predator density by predators and prey, respectively, can shape these physiological and environmental variations. This allowed analyzing how such reactions affect ecosystem stability [1].
- Energetically based models of individual growth underlie population-biological theories that range from from resource management to life-history evolution. An analysis of growth models based on allometric scaling laws found that although growth curves vary only weakly with alternative scalings, the same does not hold for reproductive outputs. As the latter are primary determinants of evolution, this highlights a non-robustness of many published evolutionary analyses and at the same time indicates how to overcome this challenge [2].
By virtue of its individual-based foundation, adaptive dynamics theory has become particularly widely used in studies interfacing ecological, evolutionary, and environmental changes:
- In ecological studies, the term “frequency independence” means that an ecological mechanism leads to a particularly simple kind of environmental feedback, allowing for easy analysis and precluding evolutionary diversification. Unfortunately, the original definition of this term by population geneticists cannot be used in realistic population dynamics. To overcome this deficiency, an ecology-based definition has been devised and shown to be equivalent to an evolutionary optimization principle [3].
- The canonical equation of adaptive dynamics theory describes the changes of heritable traits on a meso-evolutionary time scale. Using only the simplest possible mathematical tools, a new rigorous proof was constructed of the convergence of trait dynamics in a simple individual-based model to the stochastic trait substitution sequences that, for diminishing mutational step size, converge to the deterministic changes described by the canonical equation [4].
- Earlier EEP work on the canonical equation for function-valued traits was extended to models of individual development in the theory of life-history evolution [5].
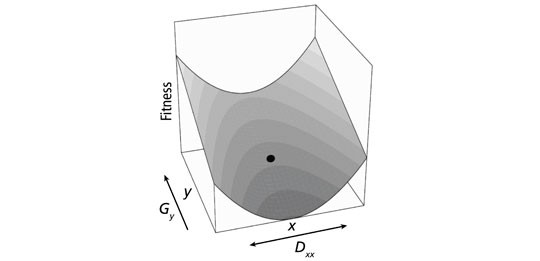
- One of the intriguing features of adaptive dynamics theory is its capacity for predicting the endogenous diversification of evolutionary traits at so-called branching points. This phenomenon is well understood for one-dimensional traits, but not for higher-dimensional ones. It has now been shown that traits around a branching point diversify in the direction of the dominant eigenvector of the selection Hessian (i.e., the matrix of second partial derivatives with respect to the mutant traits of the invasion-fitness function). This implies that, even though diversification may initially involve more than two trait values, this diversity will quickly reduce to at most two trait values [6]. In higher-dimensional trait spaces, disruptive selection may occur in one or more dimensions orthogonally to the strongest directional selection. If the latter is sufficiently stronger than the former, which always applies when mutations are sufficiently small (as assumed in the derivation of the canonical equation of adaptive dynamics theory), evolutionary diversification is prevented (Figure 1) [7].
Figure 1. Evolutionary diversification on a two-dimensional fitness landscape (grey surface) is possible only when, for average mutants around the current trait combination (black circle), disruptive selection Dxx is sufficiently stronger than directional selection Gy (click on image to enlarge).
References
[1] Sjödin H, Brännström Å & Englund G (2015). Space race functional responses. Proceedings of the Royal Society London Series B 282:20142121.
[2] Boukal DS, Dieckmann U, Enberg K, Heino M & Jørgensen C (2014). Life-history implications of the allometric scaling of growth. Journal of Theoretical Biology 359:199–207.
[3] Metz JAJ & Geritz SAH. Frequency dependence 3.0: Picking up on Heino, Metz & Kaitala (1998), in revision.
[4] Gupta A, Metz JAJ & Tran VC (2014). A new proof for the convergence of an individual based model to the trait substitution sequence. Acta Applicanda Mathematicae 121:1–27.
[5] Metz JAJ, Stanková K & Johansson J. The adaptive dynamics of life histories: From fitness-returns to selection gradients and Pontryagin’s maximum principle. Journal of Mathematical Biology, in revision.
[6] Geritz SAH, Metz JAJ & Rueffler C. Mutual invadability near evolutionarily singular strategies for multivariate traits, with special reference to the strongly convergence stable case, in revision.
[7] Ito HC & Dieckmann U (2014). Evolutionary branching under slow directional evolution. Journal of Theoretical Biology 360:290–314.

CONTACT DETAILS
Principal Research Scholar Exploratory Modeling of Human-natural Systems Research Group - Advancing Systems Analysis Program
Principal Research Scholar Systemic Risk and Resilience Research Group - Advancing Systems Analysis Program
Principal Research Scholar Cooperation and Transformative Governance Research Group - Advancing Systems Analysis Program
Research program
Eco-evolutionary Dynamics of Living Systems